Merges multiple imputed data frames into a single data frame
Source:R/merge_imputations.R
merge_imputations.RdThis function merges multiple imputed data frames from
mice::mids()-objects into a single data frame
by computing the mean or selecting the most likely imputed value.
merge_imputations(
dat,
imp,
ori = NULL,
summary = c("none", "dens", "hist", "sd"),
filter = NULL
)Arguments
- dat
The data frame that was imputed and used as argument in the
mice-function call.- imp
The
mice::mids()-object with the imputed data frames fromdat.- ori
Optional, if
oriis specified, the imputed variables are appended to this data frame; else, a new data frame with the imputed variables is returned.- summary
After merging multiple imputed data,
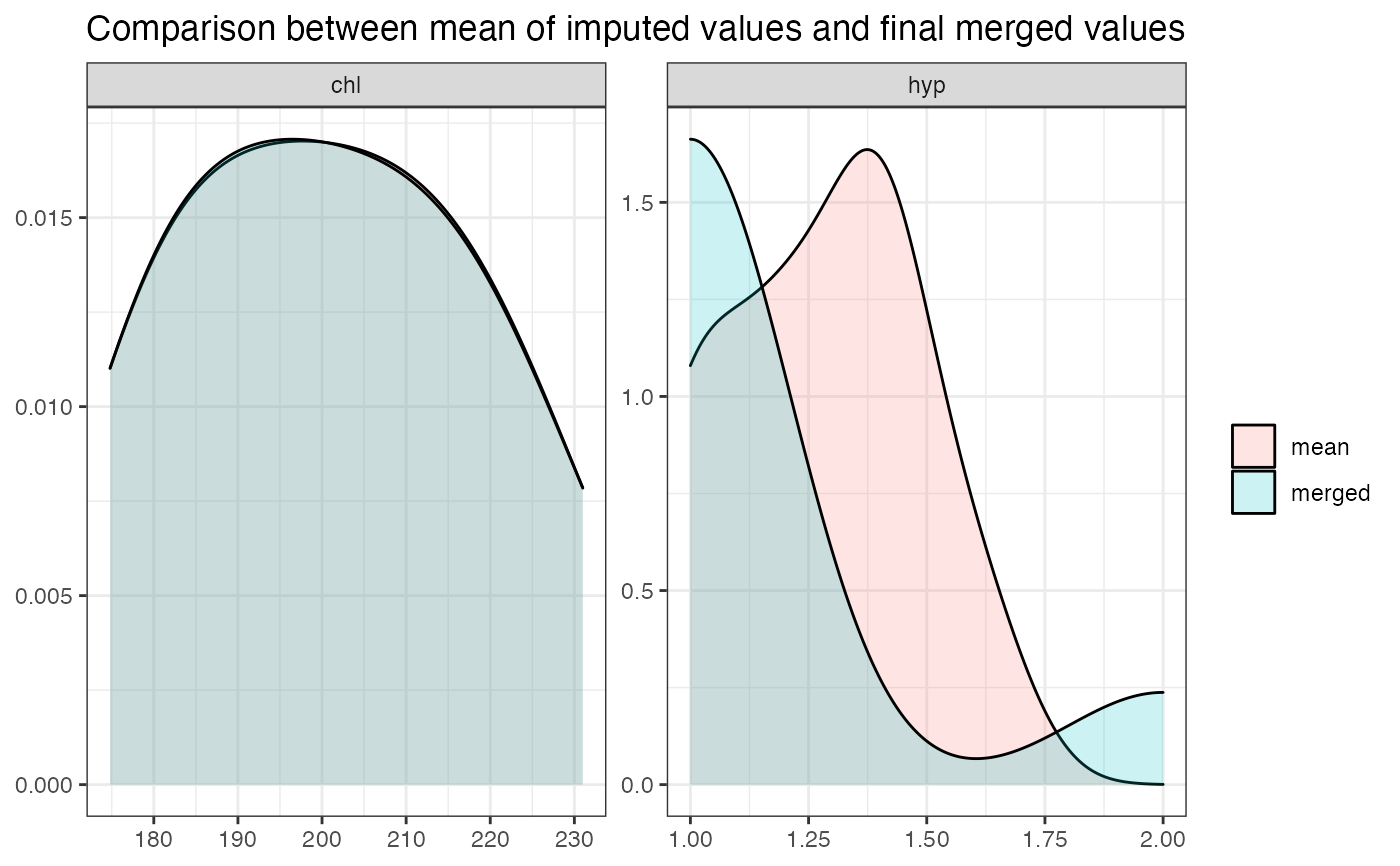
summarydisplays a graphical summary of the "quality" of the merged values, compared to the original imputed values."dens"Creates a density plot, which shows the distribution of the mean of the imputed values for each variable at each observation. The larger the areas overlap, the better is the fit of the merged value compared to the imputed value.
"hist"Similar to
summary = "dens", however, mean and merged values are shown as histogram. Bins should have almost equal height for both groups (mean and merged)."sd"Creates a dot plot, where data points indicate the standard deviation for all imputed values (y-axis) at each merged value (x-axis) for all imputed variables. The higher the standard deviation, the less precise is the imputation, and hence the merged value.
- filter
A character vector with variable names that should be plotted. All non-defined variables will not be shown in the plot.
Value
A data frame with (merged) imputed variables; or ori with
appended imputed variables, if ori was specified.
If summary is included, returns a list with the data frame
data with (merged) imputed variables and some other summary
information, including the plot as ggplot-object.
Details
This method merges multiple imputations of variables into a single
variable by computing the (rounded) mean of all imputed values
of missing values. By this, each missing value is replaced by
those values that have been imputed the most times.
imp must be a mids-object, which is returned by the
mice()-function of the mice-package. merge_imputations()
than creates a data frame for each imputed variable, by combining all
imputations (as returned by the complete-function)
of each variable, and computing the row means of this data frame.
The mean value is then rounded for integer values (and not for numerical
values with fractional part), which corresponds to the most frequent
imputed value (mode) for a missing value. Missings in the original variable
are replaced by the most frequent imputed value.
Note
Typically, further analyses are conducted on pooled results of multiple
imputed data sets (see pool), however, sometimes
(in social sciences) it is also feasible to compute the mean or mode
of multiple imputed variables (see Burns et al. 2011).
References
Burns RA, Butterworth P, Kiely KM, Bielak AAM, Luszcz MA, Mitchell P, et al. 2011. Multiple imputation was an efficient method for harmonizing the Mini-Mental State Examination with missing item-level data. Journal of Clinical Epidemiology;64:787-93 doi:10.1016/j.jclinepi.2010.10.011
Examples
if (require("mice")) {
imp <- mice(nhanes)
# return data frame with imputed variables
merge_imputations(nhanes, imp)
# append imputed variables to original data frame
merge_imputations(nhanes, imp, nhanes)
# show summary of quality of merging imputations
merge_imputations(nhanes, imp, summary = "dens", filter = c("chl", "hyp"))
}
#> Loading required package: mice
#>
#> Attaching package: ‘mice’
#> The following object is masked from ‘package:stats’:
#>
#> filter
#> The following objects are masked from ‘package:base’:
#>
#> cbind, rbind
#>
#> iter imp variable
#> 1 1 bmi hyp chl
#> 1 2 bmi hyp chl
#> 1 3 bmi hyp chl
#> 1 4 bmi hyp chl
#> 1 5 bmi hyp chl
#> 2 1 bmi hyp chl
#> 2 2 bmi hyp chl
#> 2 3 bmi hyp chl
#> 2 4 bmi hyp chl
#> 2 5 bmi hyp chl
#> 3 1 bmi hyp chl
#> 3 2 bmi hyp chl
#> 3 3 bmi hyp chl
#> 3 4 bmi hyp chl
#> 3 5 bmi hyp chl
#> 4 1 bmi hyp chl
#> 4 2 bmi hyp chl
#> 4 3 bmi hyp chl
#> 4 4 bmi hyp chl
#> 4 5 bmi hyp chl
#> 5 1 bmi hyp chl
#> 5 2 bmi hyp chl
#> 5 3 bmi hyp chl
#> 5 4 bmi hyp chl
#> 5 5 bmi hyp chl