find_beta(), find_normal() and find_cauchy() find the
shape, mean and standard deviation resp. the location and scale parameters
to describe the beta, normal or cauchy distribution, based on two
percentiles. find_beta2() finds the shape parameters for a Beta
distribution, based on a probability value and its standard error
or confidence intervals.
find_beta(x1, p1, x2, p2)
find_beta2(x, se, ci, n)
find_cauchy(x1, p1, x2, p2)
find_normal(x1, p1, x2, p2)Arguments
- x1
Value for the first percentile.
- p1
Probability of the first percentile.
- x2
Value for the second percentile.
- p2
Probability of the second percentile.
- x
Numeric, a probability value between 0 and 1. Typically indicates a prevalence rate of an outcome of interest; Or an integer value with the number of observed events. In this case, specify
nto indicate the toral number of observations.- se
The standard error of
x. Eitherseorcimust be specified.- ci
The upper limit of the confidence interval of
x. Eitherseorcimust be specified.- n
Numeric, number of total observations. Needs to be specified, if
xis an integer (number of observed events), and no probability. See 'Examples'.
Value
A list of length two, with the two distribution parameters than can be used to define the distribution, which (best) describes the shape for the given input parameters.
Details
These functions can be used to find parameter for various distributions,
to define prior probabilities for Bayesian analyses. x1, p1, x2 and
p2 are parameters that describe two quantiles. Given this knowledge, the
distribution parameters are returned.
Use find_beta2(), if the known parameters are, e.g. a prevalence rate or
similar probability, and its standard deviation or confidence interval. In
this case. x should be a probability, for example a prevalence rate of a
certain event. se then needs to be the standard error for this probability.
Alternatively, ci can be specified, which should indicate the upper limit
of the confidence interval od the probability (prevalence rate) x. If the
number of events out of a total number of trials is known (e.g. 12 heads out
of 30 coin tosses), x can also be the number of observed events, while n
indicates the total amount of trials (in the above example, the function
call would be: find_beta2(x = 12, n = 30)).
References
Cook JD. Determining distribution parameters from quantiles. 2010: Department of Biostatistics, Texas (PDF)
Examples
# example from blogpost:
# https://www.johndcook.com/blog/2010/01/31/parameters-from-percentiles/
# 10% of patients respond within 30 days of treatment
# and 80% respond within 90 days of treatment
find_normal(x1 = 30, p1 = .1, x2 = 90, p2 = .8)
#> $mean
#> [1] 53.78387
#>
#> $sd
#> [1] 30.48026
#>
find_cauchy(x1 = 30, p1 = .1, x2 = 90, p2 = .8)
#> $location
#> [1] 48.54102
#>
#> $scale
#> [1] 57.06339
#>
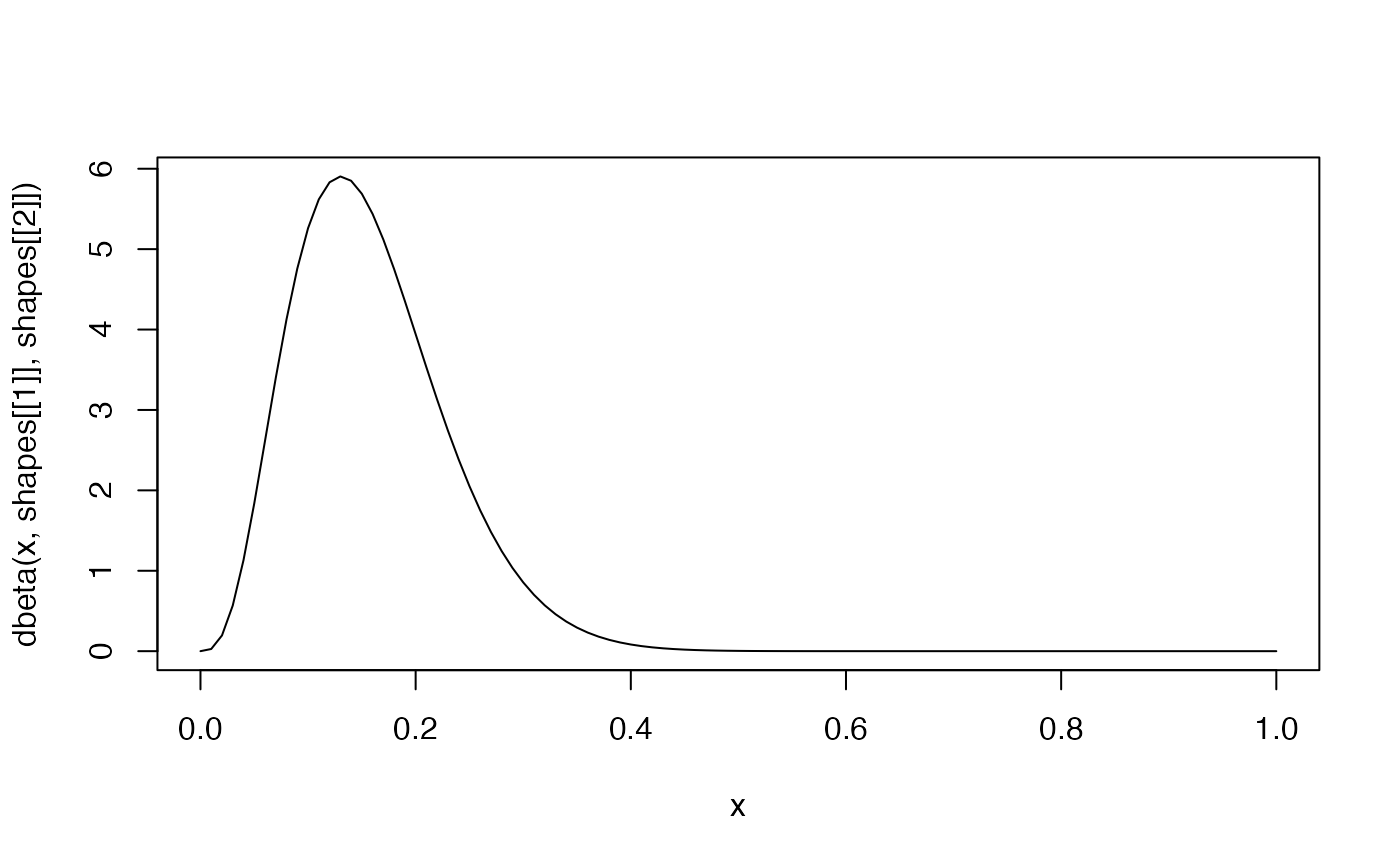
parms <- find_normal(x1 = 30, p1 = .1, x2 = 90, p2 = .8)
curve(
dnorm(x, mean = parms$mean, sd = parms$sd),
from = 0, to = 200
)
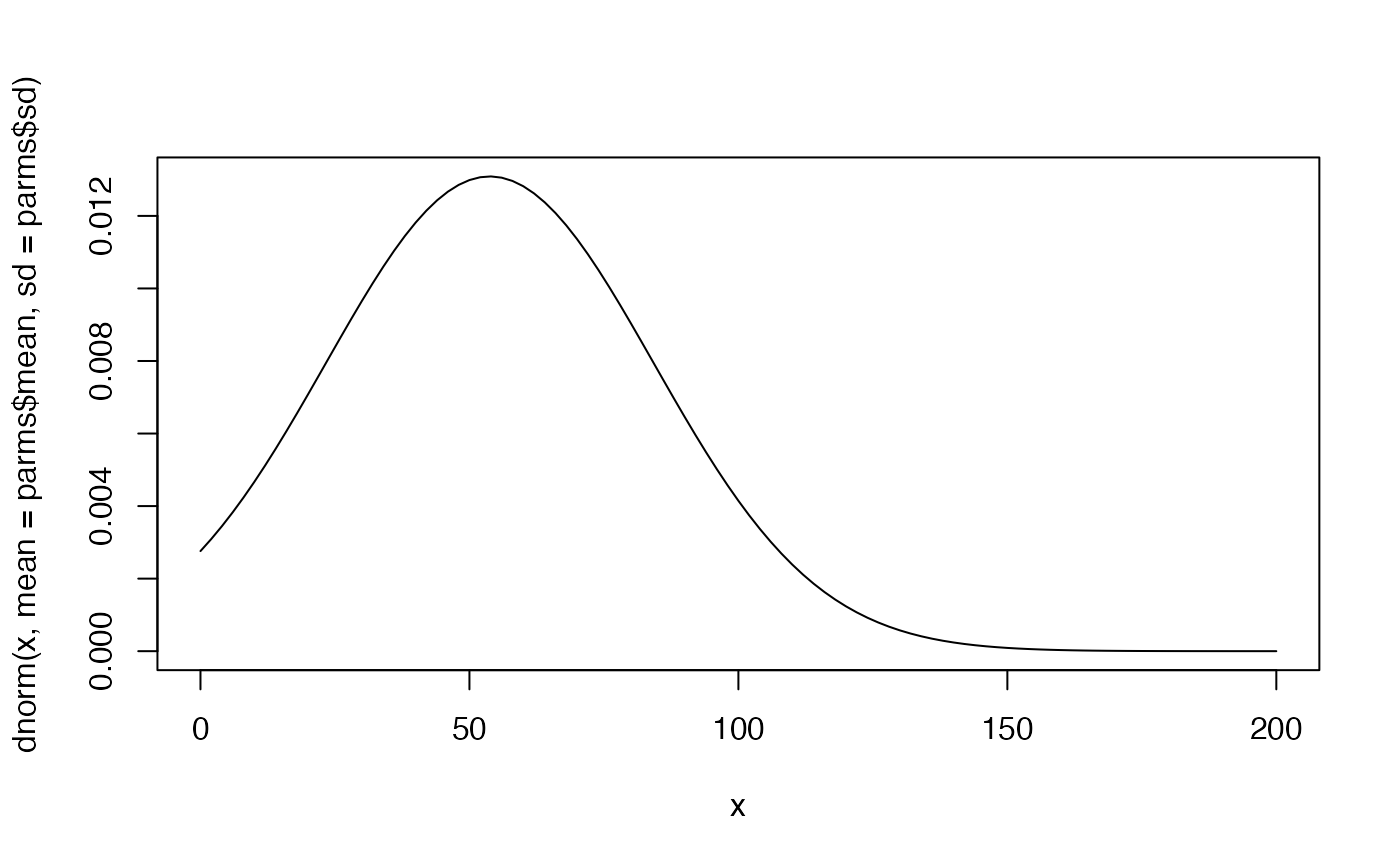 parms <- find_cauchy(x1 = 30, p1 = .1, x2 = 90, p2 = .8)
curve(
dcauchy(x, location = parms$location, scale = parms$scale),
from = 0, to = 200
)
parms <- find_cauchy(x1 = 30, p1 = .1, x2 = 90, p2 = .8)
curve(
dcauchy(x, location = parms$location, scale = parms$scale),
from = 0, to = 200
)
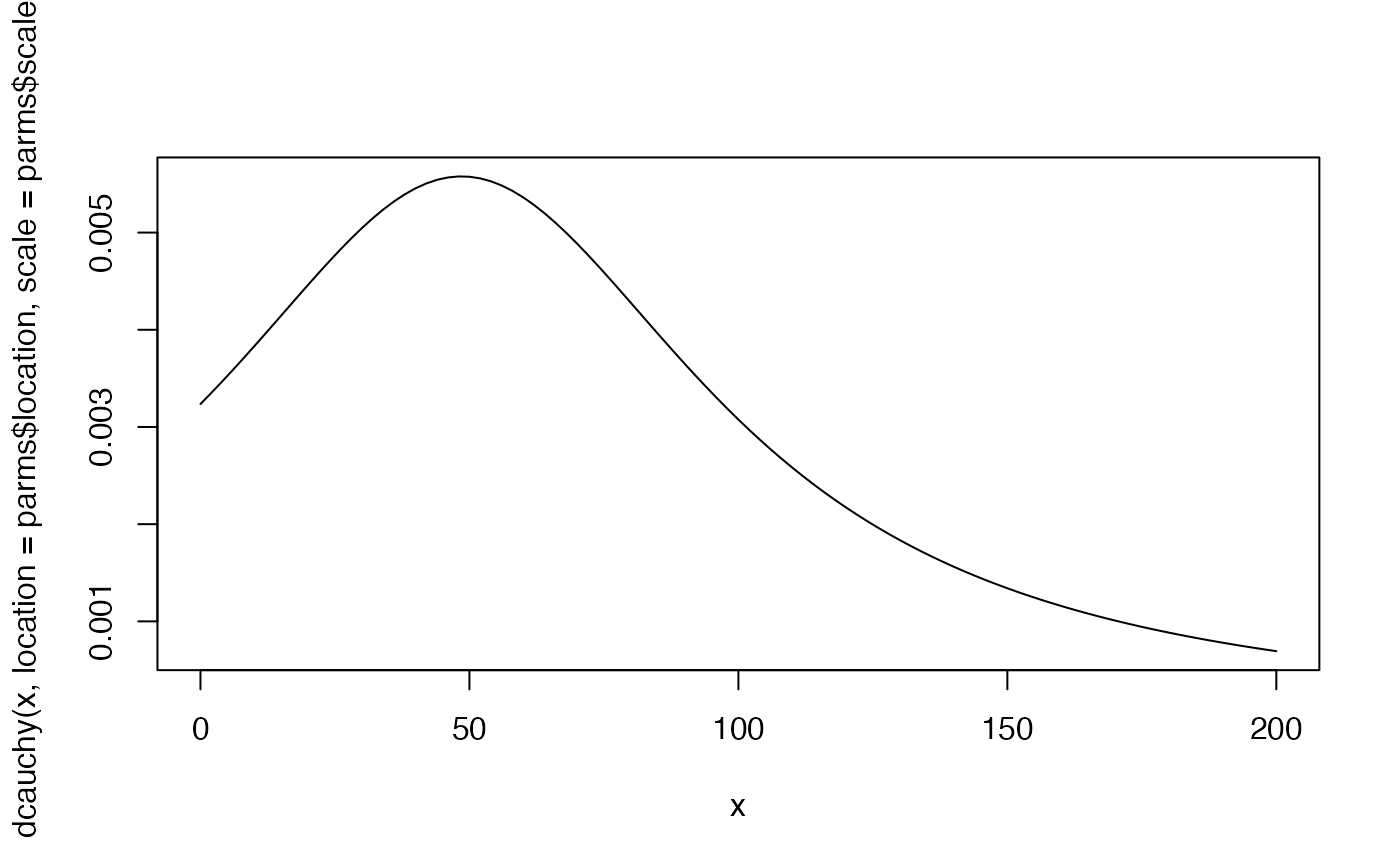 find_beta2(x = .25, ci = .5)
#> $shape1
#> [1] 2.860267
#>
#> $shape2
#> [1] 7.93757
#>
shapes <- find_beta2(x = .25, ci = .5)
curve(dbeta(x, shapes[[1]], shapes[[2]]))
find_beta2(x = .25, ci = .5)
#> $shape1
#> [1] 2.860267
#>
#> $shape2
#> [1] 7.93757
#>
shapes <- find_beta2(x = .25, ci = .5)
curve(dbeta(x, shapes[[1]], shapes[[2]]))
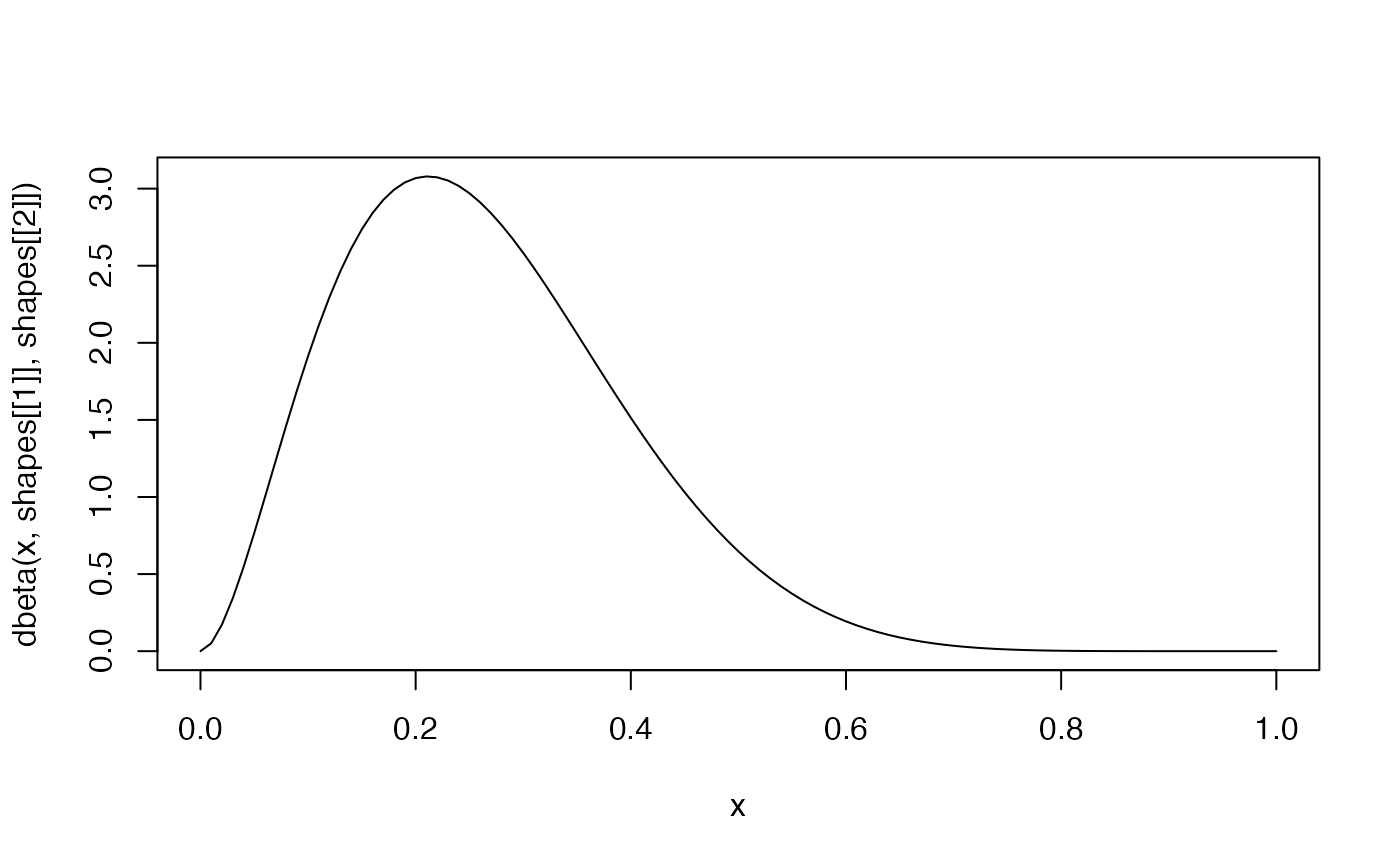 # find Beta distribution for 3 events out of 20 observations
find_beta2(x = 3, n = 20)
#> $shape1
#> [1] 4.157811
#>
#> $shape2
#> [1] 22.03272
#>
shapes <- find_beta2(x = 3, n = 20)
curve(dbeta(x, shapes[[1]], shapes[[2]]))
# find Beta distribution for 3 events out of 20 observations
find_beta2(x = 3, n = 20)
#> $shape1
#> [1] 4.157811
#>
#> $shape2
#> [1] 22.03272
#>
shapes <- find_beta2(x = 3, n = 20)
curve(dbeta(x, shapes[[1]], shapes[[2]]))