## Error in get(paste0(generic, ".", class), envir = get_method_env()) : 
##   object 'type_sum.accel' not found

This vignette demonstrate how to use ggeffects in the context of an intersectional multilevel analysis of individual heterogeneity, using the MAIHDA framework. The general approach of the MAIHDA framework (sometimes also I-MAIHDA) is described in Axelsson Fisk et al. 2018 and Evans et al. 2024.

Intersectionality analysis is a new approach in social epidemiology, which attempts to move away from looking at relevant social indicators in isolation.

“The advantage of incorporating an intersectional framework in social epidemiology is that it goes beyond the unidimensional study of socioeconomic and demographic categorizations by considering the effect of belonging to specific strata simultaneously defined by multiple social, economic and demographic dimensions.”

The steps we are showing here are:

Defining the intersectional strata.
Fitting a multilevel model to see whether intersectional strata contribute to between-stratum variance (which can be considered as “inequalities”, whether social or health related).
Fitting partially adjusted multilevel models and calculating proportional change in the between-stratum variance (PCVs) to quantify to what degree the different intersectional dimensions contribute to the between-stratum variance (inequalities).
Calculate adjusted predictions (estimated marginal means) of the outcome by intersectional strata, to get a clearer picture of the variation between intersectional dimensions, as well as testing specific strata for significant differences.

Summary of most important points:

The MAIHDA framework is a new gold standard for quantitative intersectional analysis of inequity. This approach involves multilevel modelling, where the combination of inequality dimensions (characteristics of the social strata) is included as random effect (level-2 unit).

The analysis includes following steps:

Fitting a null-model, partially and fully adjusted models. Partially adjusted models each include one of the different inequality dimenstions as fixed effect (level-1).
Calculate the ICC (also called VPC ) of the null-model to estimate the general variation between inequality dimensions.
Calculate the PCV for each partially adjusted model in comparison to the null-model, to quantify to what degree the different dimensions contribute to the inequality.
Visualize the results using adjusted predictions.

1. Prepating the data and defining intersectional strata

First, we load the required packages and prepare a sample data set. We use the efc data from the ggeffects package, which contains data of family carers who care for their elderly relatives. Our outcome of interest is quality of life of family carers (score ranging from 0 to 25 points), the different dimensions of the intersectionality groups are gender (male/female), employment status (currently employed yes/no) and age (three groups: until 40, 41 to 64 and 65 or older). We assume that there might be health-related inequalities, i.e. the quality of life differs depending on the characteristics that define our intersectional strata.

library(ggeffects)   # predictions and significance testing
library(insight)     # extracting random effects variances
library(datawizard)  # data wrangling and preparation
library(parameters)  # model summaries
library(performance) # model fit indices, ICC
library(glmmTMB)     # multilevel modelling

# sample data set
data(efc, package = "ggeffects")

efc <- efc |>
  # numeric to factors, set labels as levels
  to_factor(select = c("c161sex", "c172code", "c175empl")) |>
  # recode age into three groups
  recode_values(
    select = "c160age",
    recode = list(`1` = "min:40", `2` = 41:64, `3` = "65:max")
  ) |>
  # rename variables
  data_rename(
    pattern = c("c161sex", "c160age", "quol_5", "c175empl"),
    replacement = c("gender", "age", "qol", "employed")
  ) |>
  # age into factor, set levels, and change labels for education
  data_modify(age = factor(age, labels = c("-40", "41-64", "65+")))

To include the intersectional strata variables gender, employed and age in our mixed model, we will define them as interacting random effects (excluding main effects of interactions): (1 | gender:employed:age) (see also below). The idea is to have truly unique combinations in our model, similar as if we would create a factor variable with all combinations manually:

efc$strata <- ifelse(
  is.na(efc$employed) | is.na(efc$gender) | is.na(efc$age),
  NA_character_,
  paste0(efc$gender, ", ", efc$employed, ", ", efc$age)
)
efc$strata <- factor(efc$strata)
data_tabulate(efc$strata)
#> efc$strata <categorical>
#> # total N=908 valid N=900
#> 
#> Value              |   N | Raw % | Valid % | Cumulative %
#> -------------------+-----+-------+---------+-------------
#> Female, no, -40    |  37 |  4.07 |    4.11 |         4.11
#> Female, no, 41-64  | 238 | 26.21 |   26.44 |        30.56
#> Female, no, 65+    | 135 | 14.87 |   15.00 |        45.56
#> Female, yes, -40   |  63 |  6.94 |    7.00 |        52.56
#> Female, yes, 41-64 | 210 | 23.13 |   23.33 |        75.89
#> Female, yes, 65+   |   3 |  0.33 |    0.33 |        76.22
#> Male, no, -40      |  15 |  1.65 |    1.67 |        77.89
#> Male, no, 41-64    |  42 |  4.63 |    4.67 |        82.56
#> Male, no, 65+      |  50 |  5.51 |    5.56 |        88.11
#> Male, yes, -40     |  34 |  3.74 |    3.78 |        91.89
#> Male, yes, 41-64   |  70 |  7.71 |    7.78 |        99.67
#> Male, yes, 65+     |   3 |  0.33 |    0.33 |       100.00
#> <NA>               |   8 |  0.88 |    <NA> |         <NA>

We now have the choice and could either use the strata variable as group factor for our random effects, or gender:employed:age. For plotting predictions (see section 4), we get clearer plots when we include the three factors gender, employed and age instead of the integrated strata factor.

2. Fitting the simple intersectional model

Intersectionality analysis aims at recognizing effects of belonging to specific strata simultaneously. In the context of the MAIHDA framework, the interest lies in analysing the variation between strata regarding the outcome of interest. Thus, the indicators that define the intersectional dimensions are used as interacting random effects (group factors) in a multilevel model (random-intercept model).

We start by fitting a linear mixed effects model, which includes no fixed effects, but only our different intersectional dimensions: gender, employed and age.

# Quality of Life score ranges from 0 to 25
m_null <- glmmTMB(qol ~ 1 + (1 | gender:employed:age), data = efc)

# the above model is identical to:
# m_null <- glmmTMB(qol ~ 1 + (1 | strata), data = efc)

The purpose of this model is to quantify the “discriminatory accuracy”, which is achieved by calculating the ICC (see performance::icc()) of this model. The higher the ICC, the greater the degree of similarity within the strata (regarding quality of life) and the greater the difference in quality of life between the intersectional strata. I.e., the higher the ICC, the better the model is at discriminating individuals with higher or lower quality of life score, as opposed to models with lower ICC.

We now look at the model parameters and the ICC of our simple intersectional model.

model_parameters(m_null)
#> # Fixed Effects
#> 
#> Parameter   | Coefficient |   SE |         95% CI |     z |      p
#> ------------------------------------------------------------------
#> (Intercept) |       14.91 | 0.40 | [14.13, 15.70] | 37.41 | < .001
#> 
#> # Random Effects
#> 
#> Parameter                           | Coefficient |       95% CI
#> ----------------------------------------------------------------
#> SD (Intercept: gender:employed:age) |        1.03 | [0.56, 1.89]
#> SD (Residual)                       |        5.23 | [4.99, 5.48]

icc(m_null)
#> # Intraclass Correlation Coefficient
#> 
#>     Adjusted ICC: 0.038
#>   Unadjusted ICC: 0.038

The ICC with a value of about 4% is rather low. Usually, this indiates that our dimensions used to define the intersectional strata do not suggest larger social inequalities regarding quality of life. But we ignore this fact for now, as the purpose of demonstrating the analysis approach is rarely affected.

3. Partially-adjusted intersectional model and PCV

In the next step we want to find out, which intersectional dimension contributes most to possible inequalities, i.e. which of our group factors gender, employed and age explains most of the between-stratum variance of the random effects. This is achieved by fitting partially-adjusted intersectional models.

“The purpose of the partially adjusted model was to quantify to what degree the different dimensions used to construct the intersectional strata contributed to the between stratum variance seen in the previous model.”

For each of the intersectional dimensions, a multilevel model including this dimension as fixed effect is fitted. We can then both look at the ICCs of the partially-adjusted models, as well as at the proportional change in the between-stratum variance, the so-called PCV coefficients.

First, we fit three models each with one dimension as predictor.

m_gender <- glmmTMB(qol ~ gender + (1 | gender:employed:age), data = efc)
m_employment <- glmmTMB(qol ~ employed + (1 | gender:employed:age), data = efc)
m_age <- glmmTMB(qol ~ age + (1 | gender:employed:age), data = efc)

The regression coefficients already give an impression how strong the association between each single dimension and the outcome is, taking between-stratum variance into accout. The larger (in absolute values) the coefficients, the higher the degree that dimension contributed to the between-stratum variance.

compare_parameters(m_gender, m_employment, m_age)
#> Parameter       |             m_gender |         m_employment |                m_age
#> ------------------------------------------------------------------------------------
#> (Intercept)     | 15.55 (14.51, 16.60) | 14.23 (13.35, 15.12) | 16.25 (15.33, 17.17)
#> gender [Female] | -1.18 (-2.54,  0.17) |                      |                     
#> employed [yes]  |                      |  1.38 ( 0.07,  2.68) |                     
#> age [41-64]     |                      |                      | -1.99 (-3.14, -0.84)
#> age [65+]       |                      |                      | -2.55 (-3.88, -1.23)
#> ------------------------------------------------------------------------------------
#> Observations    |                  895 |                  895 |                  895

Looking at the summary tables above, it seems like gender is the dimension that explains least of the between-stratum variance, i.e. gender seems to be the characteristic that contributes least to potential social inequalities. age, in turn, seems to be the most important characteristic regarding inequalities.

Since the fixed effects now take away some of the proportion of the variance explained by the grouping factors (random effects), we expect the ICC for the above models to be lower.

icc(m_gender)$ICC_adjusted
#> [1] 0.02583979
icc(m_employment)$ICC_adjusted
#> [1] 0.02341412
icc(m_age)$ICC_adjusted
#> [1] 0.00461901

Indeed, the ICC correlates with the fixed effects coefficients, i.e. the larger the coefficient (in absolute values), the lower the ICC.

Next, we want to quantify the degree the different dimensions contribute to the variance between groups more accurately. To do so, we calculate the proportional change in between-stratum variance, or PCV. This coefficient explains how much of the total proportion of explained variance by the strata can be explained by a single dimension that define those strata. The PCV ranges from 0 to 1, and the closer to 1, the more this particular dimension explains social inequalities.

# extract random effect variances from all models
v_null <- get_variance(m_null)
v_gender <- get_variance(m_gender)
v_employment <- get_variance(m_employment)
v_age <- get_variance(m_age)

# PCV (proportional change in between-stratum variance)
# from null-model to gender-model
(v_null$var.random - v_gender$var.random) / v_null$var.random
#> [1] 0.3202535

# PCV from null-model to employment-model
(v_null$var.random - v_employment$var.random) / v_null$var.random
#> [1] 0.3859538

# PCV from null-model to age-model
(v_null$var.random - v_age$var.random) / v_null$var.random
#> [1] 0.8809532

Again, we see that the PCV is in line with the models’ ICC’s and regression coefficients. We see the highest proportional change for age, meaning that - although gender and education can contribute to inequalities - age is the most relevant predictor.

4. Predict between-stratum variance and test for significant differences

Finally, we may want to have a clearer picture of how the different strata vary, which combination of characteristics defines the highest or maybe lowest risk group. To do so, we calculate predictions of the random effects (unit-level predictions) by either setting margin = "empirical" or setting type = "random" (for more defaults how ggeffects handles mixed models, see this vignette.).

The following code shows the predicted average quality of life scores for the different groups.

predictions <- predict_response(
  m_null,
  c("gender", "employed", "age"),
  type = "random"
)
plot(predictions)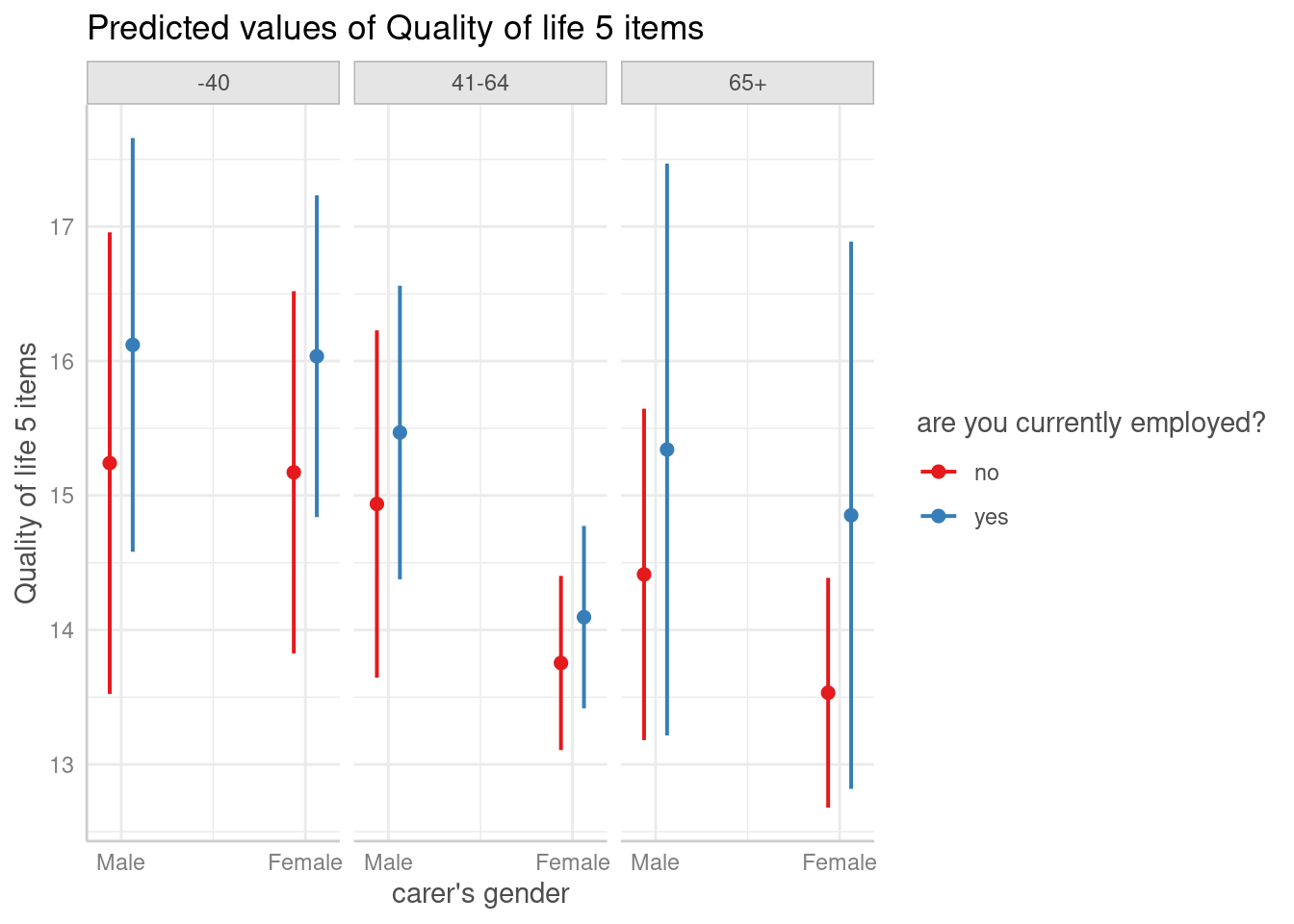

According to these results, employed male family carers, who are not older than 40 years, show on average the highest quality of life. On the other hand, unemployed female carers aged 65 or older have the lowest quality of life.

We can now calculate pairwise comparisons that show which differences between groups are statistically significant. Since all combinations of pairwise comparisons would return 66 rows in total, we just show the first ten rows for demonstrating purpose.

# just show first 10 rows of output...
test_predictions(predictions)[1:10, ]
#> # Pairwise comparisons
#> 
#> gender        | employed |         age | Contrast |      95% CI |     p
#> -----------------------------------------------------------------------
#> Female-Female |    no-no |   -40-41-64 |     1.42 | -0.08, 2.91 | 0.063
#> Female-Female |    no-no |     -40-65+ |     1.64 |  0.04, 3.23 | 0.044
#> Female-Female |    no-no |   41-64-65+ |     0.22 | -0.85, 1.29 | 0.686
#> Female-Female |   no-yes |     -40--40 |    -0.86 | -2.67, 0.94 | 0.348
#> Female-Female |   no-yes |   -40-41-64 |     1.08 | -0.43, 2.59 | 0.162
#> Female-Female |   no-yes |     -40-65+ |     0.32 | -2.12, 2.76 | 0.798
#> Female-Female |   no-yes | 41-64-41-64 |    -0.34 | -1.28, 0.60 | 0.476
#> Female-Female |   no-yes |   41-64-65+ |    -1.10 | -3.23, 1.04 | 0.313
#> Female-Female |   no-yes |     65+-65+ |    -1.32 | -3.53, 0.89 | 0.241
#> Female-Female |   yes-no |   -40-41-64 |     2.28 |  0.92, 3.64 | 0.001

If we only want to modulate one factor and compare those groups within the levels of the other groups, we can use the by argument. This reduces the output and only compares the focal term(s) within the levels of the remaining predictors.

# Compare levels of gender and employment status for age groups
test_predictions(predictions, by = "age")
#> # Pairwise comparisons
#> 
#> age = -40
#> 
#> gender        | employed | Contrast |       95% CI |     p
#> ----------------------------------------------------------
#> Female-Female |   no-yes |    -0.86 | -2.67,  0.94 | 0.348
#> Female-Male   |   no-yes |    -0.95 | -2.99,  1.10 | 0.364
#> Male-Female   |    no-no |     0.07 | -2.11,  2.25 | 0.951
#> Male-Female   |   no-yes |    -0.79 | -2.89,  1.30 | 0.457
#> Male-Female   |  yes-yes |     0.08 | -1.86,  2.03 | 0.932
#> Male-Male     |   no-yes |    -0.88 | -3.18,  1.43 | 0.455
#> 
#> age = 41-64
#> 
#> gender        | employed | Contrast |       95% CI |     p
#> ----------------------------------------------------------
#> Female-Female |   no-yes |    -0.34 | -1.28,  0.60 | 0.476
#> Female-Male   |   no-yes |    -1.71 | -2.98, -0.44 | 0.008
#> Male-Female   |    no-no |     1.18 | -0.26,  2.63 | 0.109
#> Male-Female   |   no-yes |     0.84 | -0.62,  2.30 | 0.258
#> Male-Female   |  yes-yes |     1.37 |  0.09,  2.66 | 0.036
#> Male-Male     |   no-yes |    -0.53 | -2.22,  1.16 | 0.538
#> 
#> age = 65+
#> 
#> gender        | employed | Contrast |       95% CI |     p
#> ----------------------------------------------------------
#> Female-Female |   no-yes |    -1.32 | -3.53,  0.89 | 0.241
#> Female-Male   |   no-yes |    -1.81 | -4.10,  0.48 | 0.122
#> Male-Female   |    no-no |     0.88 | -0.62,  2.38 | 0.250
#> Male-Female   |   no-yes |    -0.44 | -2.82,  1.94 | 0.717
#> Male-Female   |  yes-yes |     0.49 | -2.45,  3.43 | 0.745
#> Male-Male     |   no-yes |    -0.93 | -3.39,  1.53 | 0.459

E.g., if we look at the plot and want to know whether female persons aged 65+ differ depending on their employment status, we can use the following code:

# Compare levels employment status by gender and age groups
test_predictions(predictions, by = c("gender", "age"))
#> # Pairwise comparisons
#> 
#> employed | gender |   age | Contrast |      95% CI |     p
#> ----------------------------------------------------------
#> no-yes   |   Male |   -40 |    -0.88 | -3.18, 1.43 | 0.455
#> no-yes   |   Male | 41-64 |    -0.53 | -2.22, 1.16 | 0.538
#> no-yes   |   Male |   65+ |    -0.93 | -3.39, 1.53 | 0.459
#> no-yes   | Female |   -40 |    -0.86 | -2.67, 0.94 | 0.348
#> no-yes   | Female | 41-64 |    -0.34 | -1.28, 0.60 | 0.476
#> no-yes   | Female |   65+ |    -1.32 | -3.53, 0.89 | 0.241

5. Conclusion

Intersectional multilevel analysis of individual heterogeneity, using the MAIHDA framework, is a new approach in social epidemiology, which helps to understand the interaction of social indicators with regard to social inequalities.

This approach requires the application of multilevel models, where ICC and PCV are relevant coefficients. The ggeffects package allows to go beyond quantifying to what degree different intersectional dimensions contribute to inequalities by predicting the average outcome by group, thereby explicitly showing the differences between those groups (strata).

Furthermore, with ggeffects it is possible to compare differences between groups and test whether these differences are statistically significant or not, i.e. whether we find “evidence” for social inequalities in our data for certain groups (at risk).

References

Axelsson Fisk S, Mulinari S, Wemrell M, Leckie G, Perez Vicente R, Merlo J. Chronic Obstructive Pulmonary Disease in Sweden: An intersectional multilevel analysis of individual heterogeneity and discriminatory accuracy. SSM - Population Health (2018) 4:334-346. doi: 10.1016/j.ssmph.2018.03.005
Evans CR, Leckie G, Subramanian SV, Bell A, Merlo J. A tutorial for conducting intersectional multilevel analysis of individual heterogeneity and discriminatory accuracy (MAIHDA). SSM - Population Health (2024) 26; doi: 10.1016/j.ssmph.2024.101664

Case Study: Intersectionality Analysis Using The MAIHDA Framework